이진 탐색 알고리즘 역시 시간복잡도를 알아보고자 한다. 그리고 이전에 알아본 순차 탐색 알고리즘에 비해 얼마나 효율적인지도 시간복잡도를 통해 알아본다.
여기서 알아볼 시간복잡도는 최악의 경우만을 따진다. 최선의 경우는 한 번이고, 평균적인 경우는 따지기가 몹시 애매하기 때문이다. 아니, 솔직히 말하면 그냥 어려워서다. 나중에 알아보도록 하자. 여기선 오직 최악의 경우(Worst case)만을 다루도록 하겠다.
최악의 경우(Worst case) 시간복잡도
데이터의 개수가 n개인 경우, 이진 탐색 알고리즘을 이용했을 때의 연산 경우의 수는 아래와 같이 일반화할 수 있다.
1. n이 1이 되기까지 2로 나누고 나머지를 버린다. 비교연산 횟수 총 k회
2. n이 1이 되었을 때, 마지막 비교연산 1회
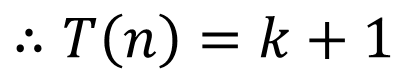
이제 k를 n에 관한 식으로 만들어야 한다. k는 앞서 설명했는데 n을 2로 나눠 1이 만들게 하는 숫자다. 수학에 익숙한 이과분들은 그냥 스크롤을 내려서 다음 식을 바로 확인하면 된다. 그러나 나는 수학을 못하는 관계로 차근차근 알아보자.
위에 했던 말을 그대로 n, k로 이루어진 수학식으로 만들어보자
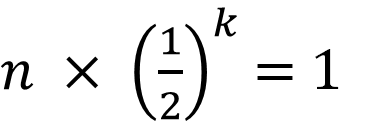
n을 k번만큼 2로 나누었더니 1이 되었다. 그럼 마지막으로 이걸 k= 꼴로 정리하자면
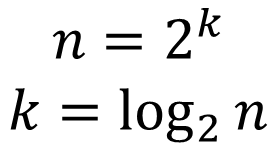
똑똑한 분들이었다면 위의 2가지 일반화 가정을 보자마자 이 식을 떠올렸을 것이다. 그치만... 나눈 그런고 모탄다ㅎㅎ
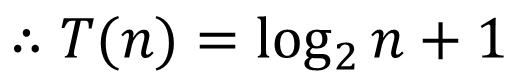
위와 값이 최악의 경우의 시간복잡도를 구했다. 그렇다면 다시 한 번 앞에서 구현한 이진 탐색 알고리즘을 조금 고쳐서 위의 공식을 검증하고 직접 눈으로 확인해보자.
구현
#include <iostream>
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <functional>
using namespace std;
vector<int> v;
int compare = 0;
void BinSearch(int target)
{
int first = 0;
int last = v.size() - 1;
int mid;
while (first <= last)
{
mid = (first + last) / 2;
if (target == v[mid])
{
compare++;
if (compare < 10)
cout << " ";
cout << " #" << compare << " : " << target << " = " << v[mid] << " / n = " << last - first + 1 << "\n";
return;
}
else if (target < v[mid])
{
compare++;
if (compare < 10)
cout << " ";
cout << " #" << compare << " : " << target << " < " << v[mid] << " / n = " << last - first + 1 << "\n";
last = mid - 1;
}
else
{
compare++;
if (compare < 10)
cout << " ";
cout << " #" << compare << " : " << target << " > " << v[mid] << " / n = " << last - first + 1 << "\n";
first = mid + 1;
}
}
return;
}
int main()
{
cin.tie(NULL);
cout.tie(NULL);
ios::sync_with_stdio(false);
int size, temp;
cout << " Enter array size : ";
cin >> size;
cout << "\n";
for (int i = 0; i < size; i++)
v.push_back(i);
BinSearch(size+1);
cout << "\n Time complexity : " << compare << "\n\n";
return 0;
}
간략 코드 설명
주석을 다는 것보다는 말로 설명하고 직접 코드를 보시는게 편하리라 생각된다.
배열데이터의 각 원소는 배열번호와 같다. 예를 들어 10개짜리 배열을 만들면 arr[0]~arr[9]까지 0~9가 순서대로 입력된다. 그리고 이진 탐색 함수에서는 배열에서 가장 큰 숫자보다 1큰 숫자를 탐색시킬 것이다. 위의 경우를 예를 들면 10을 검색시키는 것이다. 그렇게 하면 무조건 최악의 경우로 가게 된다.
실행결과
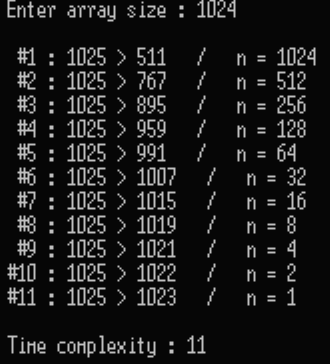
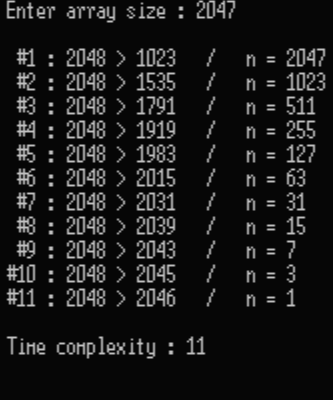
1024와 2047 둘 다 log_2를 취하면 10이 나온다. 2047은 소숫점이 있지만 이진 탐색 과정에서 소숫점은 모두 무시하기 때문에 결국 둘 다 같은 결과가 나왔다. 위에서 구한 시간복잡도대로 10+1=11.
순차 탐색 vs 이진 탐색
애초에 이진 탐색은 정렬된 데이터를 탐색하는 반칙을 사용하는데 더 효율적이지 않으면 안되는 일이다. 결과는 예상대로 이진 탐색이 훨씬 빠르다.
순차 탐색의 평균 시간복잡도와 이진 탐색의 최악의 시간복잡도를 비교해보자.
1. 순차 탐색 알고리즘 평균 시간복잡도 (탐색 데이터는 100% 배열 중에 존재)
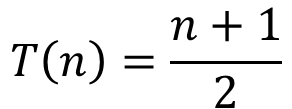
2. 이진 탐색 알고리즘 최악의 경우 시간복잡도
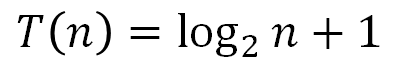
n이 곧 비교연산 횟수이자 곧 연산시간이므로, 값이 작은 쪽이 효율적인 알고리즘이다. 그렇다면 n이 몇 이상일 때부터 이진 탐색 알고리즘의 값이 더 작아지는지 알아보면 된다.
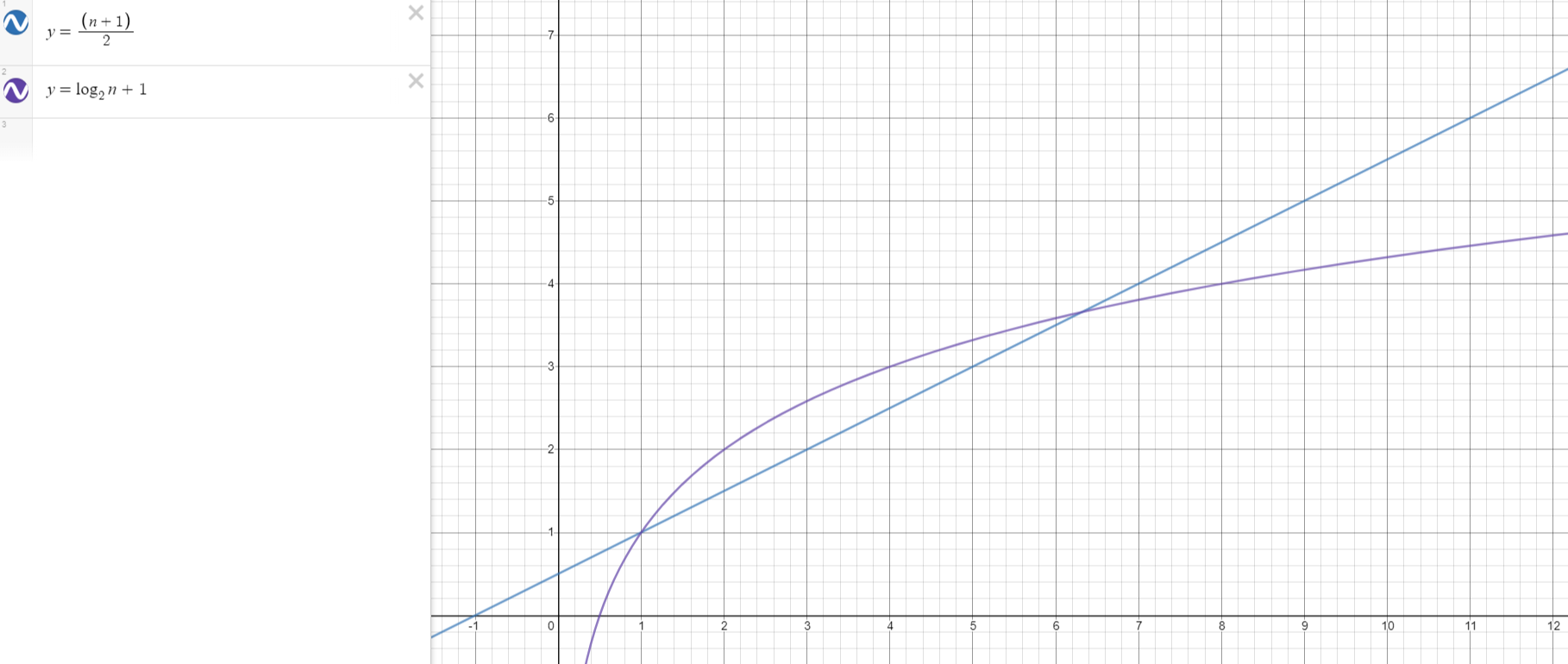
n이 1에서 6사이일때 까지는 순차 탐색이 더 효율적이지만, 그 이후부터는 이진 탐색이 더 빨라진다. 더군다나 데이터의 크기가 커질수록 그 격차는 기하급수적으로 벌어진다. 이와 관련해 더 공부하고 싶으신 분들은 빅-오 표기법 (Big-O Notation)에 대해서 공부하면 좋다.
'컴퓨터 > 자료구조' 카테고리의 다른 글
| [자료구조 / C++] 이진 탐색 알고리즘 (Binary Search Algorithm) (1) | 2019.07.25 |
|---|---|
| [자료구조/C++] 순차 탐색 알고리즘 평균 시간 복잡도 (Linear Search Algorithm Average Time Complexity) (1) | 2019.07.24 |
| [자료구조/C++] 순차 탐색 알고리즘 (Linear Search Algorithm) (2) | 2019.07.24 |
